This little guy craves the light of knowledge and wants to know why 0.999… = 1. He wants rigour, but he does accept proofs starting with any sort of premise.
Enlighten him.
if 0.333… = 1/3 then 0.999… = 3/3 = 1
lots of good proofs in this thread but this one gets points for being by FAR the shortest while still being completely based on intuition and makes complete sense with an average high school mathematics background
The thing that really got 0.999…=1 to click on my mind is the fact that you can’t find a number between 0.999… and 1. You might think “Just put something at the end of 0.999…,” but there is no end to 0.999…
Yay, Dedekind cuts are finally useful!
deleted by creator
Yeah that’s something that people have to get used to in maths, if the limit of a sequence exists we can just pretend to have “reached infinity” and work with like any number
I’m not sure what you are trying to say here, and I have a background in math. I think this is just going to confuse lay people.
Im trying to make the distinction between a function that approaches a value as it’s input grows, for instance a sequence seen as a function on the domain of the natural numbers, and the value itself.
I have seen a lot of people view 0.999… as a number that “approaches one”, so formally speaking as the sequence (0.9, 0.99, 0.999, …) and not the number itself which that sequence approaches which they would agree is 1.
The “its the largest number which is less than 1” type of thinking.
I am going to note that this was not well-expressed when you said ‘we can just pretend to have “reached infinity” and work with like any number’. To a lay person it would look as if you were suggesting that we non-rigorously treat one object (like the sequence (0.9, 0.99, 0.999,…)) as another (like the real number that that sequence converges to given the standard topology of the space of real numbers).
I’m not really confused about what you’re saying here exactly, and since the original post is deleted, I can’t really even see what was originally said, but I was confused about this:
(like the real number that that sequence converges to given the standard topology of the space of real numbers).
Why make mention of the standard topology here exactly? It’s not exactly clear to me why this has anything to do with what you two are discussing.
Just to be specific, as what a particular sequence converges to depends on the topology of the space where we are looking for a limit of the sequence. Hell, in non-Hausdorff spaces a sequence can have multiple limits (trivial case: anti-discrete space of cardinality greater than 1 will have every sequence converge to every point in it).
Thanks for the clarification! In my mind, I sort of just think “metric first” so the topology induced by that metric is always just assumed, but that’s because I don’t ever work with non-metrizable spaces.
and wants to know why 0.999… = 1
\begin{align} 0.999… &= 9\cdot(0.1+0.01+0.001+… ) \ &= 9\cdot( 0.1^1 + 0.1^2 + 0.1^3 + … ) \ &= 9\cdot(\sum\limits_{k=1}^\infty ( \frac{1}{10^k} ) ) \ &= 9\cdot(\sum\limits_{k=0}^\infty ( \frac{1}{10^{(k+1)}}))\ &= 9\cdot(\sum\limits_{k=0}^\infty \frac{1}{10}*(\frac{1}{10^k})) \ &= \frac{9}{10}\cdot (\sum\limits_{k=0}^\infty (\frac{1}{10^k})) \ &= \frac{9}{10}\cdot \frac{1}{(1-(\frac{1}{10}))}\ &= \frac{9}{10}\cdot \frac{10}{9} = 1 \end{align}
The crux rests on a handy result on from calculus: the sum of an infinite geometric series looks likes s = 1/(1-r), when s = \sum\limits_k=0^inf r^k, and |r| < 1.
Sorry for the latex. When will hexbear render latex? This is a bit more readable:
(aesthetic edit for our big beautiful complex analysts)
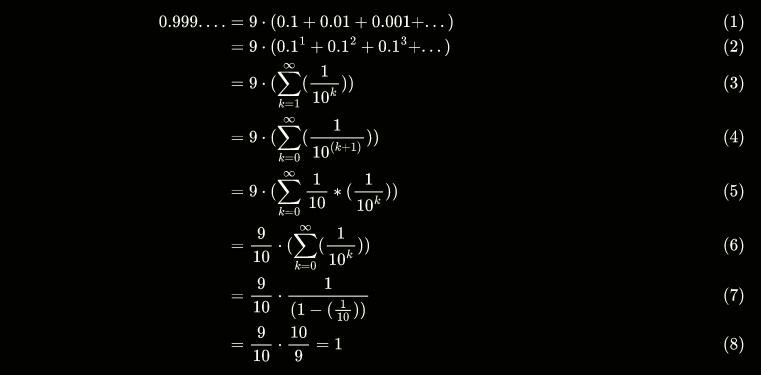
Never thought of employing the geometric series for this, that’s clever.
^_^ thank you!
Using i as an index 🤮
? Thats pretty standard though right?
in computer programs, yes
not so much in analysis
I’m seeing n and i used as variables in Rudin, predominantly n though, but Im accustomed to n being a constant.
The symbol ‘i’ is usually reserved for the imaginary unit.
I’ve seen it used very frequently as a name for a variable, the imaginary unit i usually has a different typeface to distinguish the two is what Im accustomed to.
Your feedback is valid and I apologize for rendering such an ugly proof
And doesn’t this mean 0.99 approaches 1
A real number can’t be approaching anything. It is not a function or any other sort of object that can be said to be approaching anything.
No. 0.99 is 0.9+0.09. The proof I gave shows that 0.99999999999999999999999999999999999(…) is equal to 1.
K
so, start with:
x = 0.999…
now multiply each side by 10
10x = 9.9999…
now we subtract x from the left side, and 0.999… from the right, which is fine because they are equal:
9x = 9
and from there it should be fairly obvious that x is also equal to 1, which means 0.999… is also equal to 1
0.999…=1 because it’s funny that people get so mad about it
I agree, but the little guy does need rigour, or he will starve under crapitalism.
I didn’t have any bread to bring him but I had plenty of roses
I suppose I will post one myself, as I do not expect anybody else to have that one in mind.
The decimals ‘0.999…’ and ‘1’ refer to the real numbers that are equivalence classes of Cauchy sequences of rational numbers (0.9, 0.99, 0.999,…) and (1, 1, 1,…) with respect to the relation R: (aRb) <=> (lim(a_n-b_n) as n->inf, where a_n and b_n are the nth elements of sequences a and b, respectively).
For a = (1, 1, 1,…) and b = (0.9, 0.99, 0.999,…) we have lim(a_n-b_n) as n->inf = lim(1-sum(9/10^k) for k from 1 to n) as n->inf = lim(1/10^n) as n->inf = 0. That means that (1, 1, 1,…)R(0.9, 0.99, 0.999,…), i.e. that these sequences belong to the same equivalence class of Cauchy sequences of rational numbers with respect to R. In other words, the decimals ‘0.999…’ and ‘1’ refer to the same real number. QED.
I like how compact this one is ;)
Had a little trouble following this as plain text, so I wrote it up in LaTeX (it’ll be a bit small if you try to read it inline–you’ll probably want to tap to enlarge on mobile or open the image in a new tab/click this direct link to the image):

I tried to hew as closely to your notation as I could, but let me know if you spot any errors!
Thank you.
And no, I do not notice any errors.
I should re-learn Lateχ.
Doesn’t that just mean they’re both elements of a Cauchy sequence rather than equivalent? I suck at maths.
Not quite. The wording “equivalence classes of … with respect to the relation R: aRb <==> lim( a_n - b_n) as n->inf” is key.
https://en.wikipedia.org/wiki/Equivalence_class
loosely, an equivalence relation is a relation between things in a set that behaves the way we want an equal sign to
For an element in a set, a, the equivalence class of a is the set of all things in the larger set that are equivalent to a.
lol I hate math so much
“Having the same age” is an equivalence relation between people.
-
It is reflexive: Bob is always the same age as himself
-
It is symmetric: if Bob is the same age as Sally, then Sally is the same age as Bob
-
It is transitive: If Bob is the same age as Sally, and Sally is the same age as Fred, then Bob is the same age as Fred.
using symbols:
Bob ~ Bob Bob ~ Sally ⇒ Sally ~ Bob Bob ~ Sally and Sally ~ Fred ⇒ Bob ~ Fred“⇒” means “the statement on the left implies the statement on the right.” When people in this thread write =>, <=, and <=> they mean ⇒, ⇐, and ⇔
An “equivalence class” is the set of all items that obey the equivalence relation with each other. So, “being 25 years old” is an equivalence class containing every person who is 25 years old. Those people might be different in every other way, but they are equivalent in that specific regard.
In their proof earlier, @Tomorrow_Farewell@hexbear.net defined two equivalence classes. Instead of “people who are 25 years old,” the classes were “infinite sequences that converge to 1” and “infinite sequences that converge to 0.999…” They showed that these are the same class.
Great explanation thanks
-
So, under the relevant construction of the space of real numbers, every real number is an equivalence class of Cauchy sequences of rational numbers with respect to the relation R outlined in my comment. In other words, under this definition, a real number is an equivalence class that includes all such sequences that for every pair of them the relation R holds (and R is, indeed, an equivalence relation - it is reflexive, symmetric, and transitive, - that is not hard to prove).
We prove that, for the sequences (1, 1, 1,…) and (0.9, 0.99, 0.999,…), the relation R holds, which means that they are both in the same equivalence class of those sequences.
The decimals ‘1’ and ‘0.999…’, under the relevant definition, refer to numbers that are equivalence classes that include the aforementioned sequences as their elements. However, as we have proven, the sequences both belong to the same equivalence class, meaning that the decimals ‘1’ and ‘0.999…’ refer to the same equivalence class of Cauchy sequences of rational numbers with respect to R, i.e. they refer to the same real number, i.e. 0.999… = 1.
He’s hungry

Feed himI will be posting another another proof, one using the assumption that 0.999… is the sum of the series 9/10+9/100+9/1000+… (and that 1 is the sum of the series 1+0+0+0+…), unless somebody else comes here and feeds it to the little guy first.
(I haven’t done real math since forever)
Part 1: Proving If x,y are distinct positive real numbers and x < y, there is a z in R such that x < z < y.
Let y = x + e, where e is in R. e is also positive because:
x < y
x < x + e
0 < ex < z < y becomes x < z < x + e. We can then choose z = x + 0.5e so that
x < z < y
x < x + 0.5e < x + e
0 < 0.5e < e
0.5e - 0.5e < 0.5e + 0 < 0.5e + 0.5e
-0.5e < 0 < 0.5eSince we’ve shown earlier that e > 0, -0.5e < 0 < 0.5e is true no matter what e.
Part 2: Decimal Notation
Decimal notation is written as the sequence amam-1…a1a0.b1b2…bn, where a,b are in the set {0,1,2,3,4,5,6,7,8,9}. The sequence amam-1…a1a0.b1b2…bn itself is of the number am10m + am-110m-1 + … + a0100 + b110-1 + b210-2 + … + bn10-n.
Part 3: The actual proof through proof by contradiction
Let x = 0.999… and y = 1. This means there exists a z that is between 0.999… and 1. So let’s construct z = a0.b1b2…bn. a0 has to be either a 0 or 1 and since there is no number smaller than 1 with 1 as its first digit, a0=0. z = 0.b1b2…bn
0.999… = 9*10-1 + 9*10-2 + 9*10-3 + … while z = b110-1 + b210-2 + … + bn10-n. If 0.999… < z, then
0.999… - z < 0
9*10-1 + 9*10-2 + 9*10-3 + … - (b110-1 + b210-2 + … + bn10-n) < 0
(9*10-1 - b110-1) + (9*10-2 - b210-2) + (9*10-3 - b310-3) + … < 0
(9 - b1)*10-1 + (9 - b2)*10-2 + (9 - b3)*10-3 + … < 0But as we’ve established in Part 2, b1, b2, b3, etc have to be from the set {0,1,2,3,4,5,6,7,8,9}, meaning (9 - bn) > 0 for any n. Therefore, (9 - b1)*10-1 + (9 - b2)*10-2 + (9 - b3)*10-3 + … cannot be less than 0.
The theorem requires for x and y to be distinct positive real numbers and x < y, and since 0.999… and 1 can be trivially shown to be positive real numbers, this means that 0.999… and 1 are not distinct. In other words, 0.999… = 1.
Alright, so, the other proof that I promised:
If we define 0.999… as the sum of the series 9/10+9/100+9/1000+…, then for every neighbourhood U(1) it is true that there exists a metric ball B_N = B(1, 1/10^N), where N is natural, such that B_N is a subset of U(1).
For all natural n > N it is true that d(sum(9/10^k) for k from 1 to n, 1) = |1 - sum(9/10^k) for k from 1 to n| = |1/10^n| = 1/10^n < 1/10^N, meaning that for all natural n > N it is true that sum(9/10^k) for k from 1 to n is in B_N, meaning that it is also in U(1).
However, sum(9/10^k) for k from 1 to n is the nth partial sum of the series 9/10+9/100+9/1000+…, which, together with the fact that every such sum is in U(1) for n > N, means that 1 is the limit of the sequence of the partial sums of the series 9/10+9/100+9/1000+…, meaning that 1 is the sum of that series. That means that 0.999… is 1 by definition.
The ellipses mean infinity. Anything less than infinity and the equation is false. It looks unintuitive because infinity is unintuitive
The ellipses mean infinity
No, it does not. The ellipsis notation is used to denote a repeating pattern. It is not used to denote points that are named ‘infinity’ in spaces like Aleksandrov compactification and the extended space of real numbers.
I am sorry, but your reply lacks rigour.
Is this a bit? I meant that the ellipses, in this context, mean that the nines go on forever. Obviously there are other symbols used to represent similar ideas, like ∞
I’m being serious. The word ‘infinity’ refers to some points from spaces like Aleksandrov compactification. It does not refer to any sort of repetition of any pattern. You cannot, for example, write ‘0.999∞’ or ‘0.999infinity’ to mean the same thing as ‘0.999…’ or ‘0.(9)’.
ok mothematician








