I’m learning game theory these days, and I’ve tried my hand at some problems inspired by ML theory. Here’s one I found really interesting.
Let’s assume the following (clearly unrealistic) situation:
- Working class (A) and bourgeoisie (B) form perfectly cooperative coalitions.
- They may negotiate salaries, with no class having any mechanism to obtain a better bargaining position.
- A cooperatively owns some amount k of capital, while B owns (arbitrarily) 1. In principle, k < 1.
- B has some labor power b, while A has (arbitrarily) 1. Again, b < 1.
- Production follows a Cobb-Douglas function, where the sum of the output elasticities of capital and labor is 1.
- Both classes consume the same proportion of their income and use the remainder to acquire more capital.
Therefore, the payoffs in our problem can be stated like this (where w is the labor given to B and s is the compensation given to A for this labor):
X_A = A k**α (1 - w)**β + s
X_B = A (b + w)**β - s
We would like to find how the ratio of A’s capital to B’s changes over time, so we compute its derivative using the quotient rule, and note that the proportion of income (p) spent on capital is the same for both classes:
R = p X_A - k p X_B
Finally, we find the Nash equilibrium and its corresponding R at each combination of k and b:
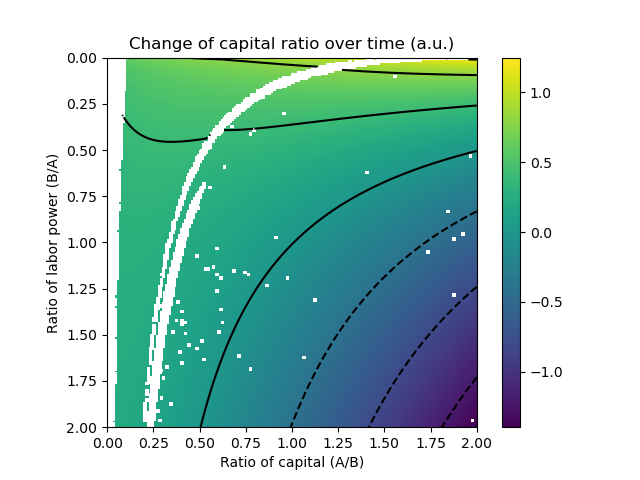
Note the attractor curve coinciding with k = 1/b. In other words, if both k and b are higher than 0, the eventual equilibrium will be for A and B to own capital proportional to their labor power.
Edit: fixed some missing solutions near k = 0.


It’s the quotient rule for derivatives.